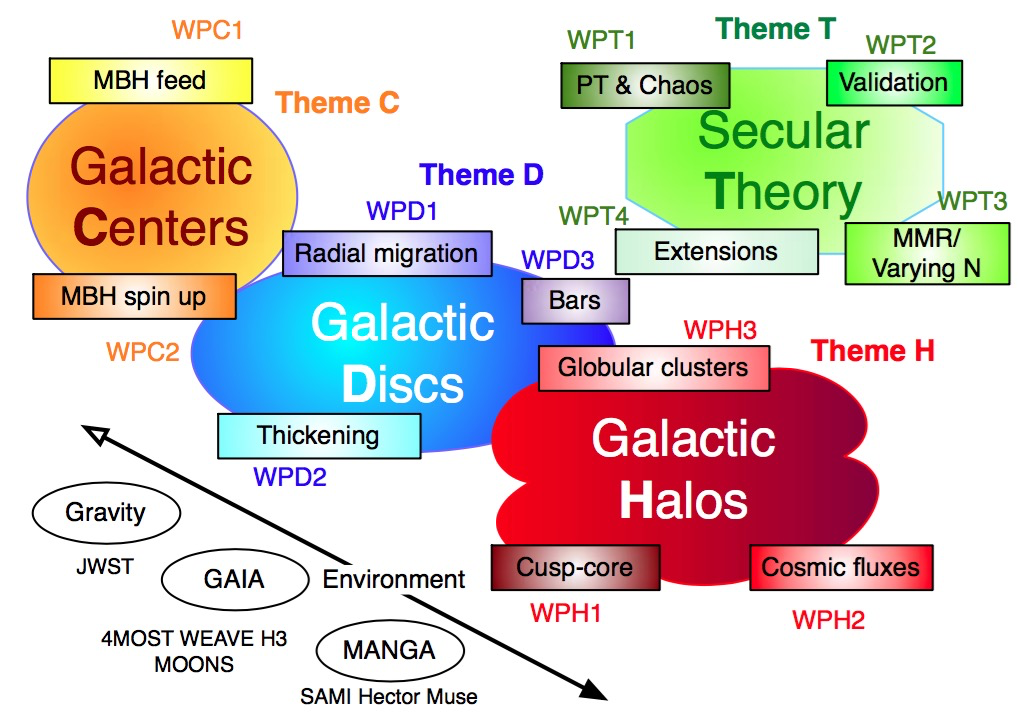
Secular Theory
Secular-T theory for self-gravitating systems
The kinetic theory of gravitating systems is a very active and fruitful field of research, as illustrated by Villani’s’10 Fields medal, or Mouhot’s’16 Adams prize for their “link between kinetic theory and molecular dynamics... and the relaxation towards equilibrium for collisional equations of Boltzmann type”. One of the purposes of SEGAL will also be to continue stimulating theoretical physics with novel kinetic theories arising in the context of galactic dynamics and 'gravitational plasma physics'. In this work-package, we will address some of the limitations of the existing kinetic theories, validate our findings using alternative methods, and investigate how our extended kinetic equations can be generalised to describe wider classes of dynamical processes, on both shorter and longer timescales.
WPT1: At first order, in the previous themes, we assumed integrability, i.e. the existence of global angle-action coordinates. It can be either guaranteed by the system’s symmetry (spherical halo, razor-thin discs) or by additional assumptions, such as the epicyclic approximation. When it does not hold, the system’s dynamics may become partially chaotic and its secular evolution may need to be described via explicit stochastic diffusions, which we will need to calibrate from simulations. For example, for stellar discs, chaos is likely to play a role in the central bar. In SEGAL, we will rely on perturbation theory (Goldstein’50) to build new (fast and slow) angle-actions customized to each resonance, using as a perturbation the departure from symmetry of the sought system: this strategy, known as Torus Mapping (Binney+’16), yields new actions with which secular diffusion will be reformulated. We will in particular build secular diffusion equations for thickened discs models and triaxial cusps. Eventually, it would be of significant interest to account for the anisotropy of the environment as well (following e.g. Aubert+’04).
WPT2: When implementing complex kinetic theories with loopback via self-gravity, validation is essential. Since we aim to make SDE solution a competitive tool to N-body simulations, we must demonstrate that the kinetic formulation accurately describes the secular response of modelled systems. Relying on ColDICE, a state-of-the-art public Vlasov (waterbag) solver developed at IAP (via our Vlasix project), we will compare the effect of secular evolution accurately described by such codes to the prediction of N-body on the one hand, and kinetic theory using SDE on the other hand. We will also rely on FEM for comparison, relying on the (hired) expertise of the PDF, and the PI and CoI upcoming investment in this technology (using the discontinuous Galerkin method). This comparison will also be used to study and understand the process of entropy production, having access via kinetic theory to an explicit analytic expression for its rate. It will allow us to study secular dynamical phase transitions (Fouvry+’15), which capture the slow and irreversible build-up of collisional effects leading to a destabilisation of secularly metastable states. At the technical level, the IBL equation can be used to quantify numerical shot-noise errors occurring in N-body codes, and partially controled in Vlasov codes such as ColDICE. Conversely, ColDICE can be used to study coherent transients in phase space, as seen by GAIA.
WPT3 The derivation of the existing resonant orbital kinetic equations assumes full phase-average. They do not in their present form capture commensurability in the orbital frequencies (such as the 2:3 Pluto–Neptune resonances in our solar system) and are only concerned with orbit-orbit interactions. We will investigate in SEGAL how the secular formalism can be generalized to include such mean-motion resonances, following the procedure implemented for the Keplerian problem (i.e. integration over the fast angle before closure). SEGAL will also investigate how kinetic theory can be generalized to systems with a small or fluctuating number of effective particles, for example as a result of the progressive dissolution of over-densities. This will allow us to explore intermediate timescales, when the system has not fully phase mixed nor violently relaxed. We will attempt to develop a theory for the rate of entropy production, while distinguishing the rapidly rising phase from the asymptotic one.
WPT4 In some regimes, the resonant orbital diffusion described by the IBL equation may vanish or weaken significantly. This can for example occur in galactic centers, as illustrated by the Schwarzschild barrier, driven by the divergence of the relativistic precession frequencies as stars move closer to the BH. This vanishing can also be imposed by symmetry, e.g. the collision operator vanishes for 1D homogeneous systems. Finally, it may happen on longer secular timescales if steady states for the IBL equation have been reached by the system. In such regimes, additional collisional effects involving three-body resonances will be accounted for within SEGAL. In addition to strong collisions, resonant effects associated with 1/N2 correlations can also drive the dynamics. This requires to consider the third equation of the BBGKY hierarchy and focus on slower effects associated with 3−body correlations. SEGAL will generalise the functional derivation of the inhomogeneous Landau equation (Fouvry+’16a) to account for collective effects and re-derive the IBL equation. This derivation will be challenging, as it involves a Fredholm integral equation for closure, but it is potentially very useful, since path integrals can easily be tailored to variational principles, which should help us formalise optimal FEM solutions. SEGAL will also apply this method to derive a closed kinetic equation involving higher order correlations. This could for example allow us to describe the dynamics of 1D homogeneous systems, for which the 1/N IBL collision term vanishes by symmetry (Eldridge+’63). It is also relevant for the Hamiltonian Mean Field toy model (HMF) (Bouchet +’05), the archetype of bar instability in galaxies. Finally, kinetic equations such as the Balescu equation describe the most probable evolution of the one particle distribution function through the law of large numbers. Following recent developments in non-equilibrium statistical mechanics, we will attempt to describe rare-event fluctuations away from this most likely PDF using Large Deviation Theory (e.g. Saint-Raymond’09, Codis+’15).

Results & Deliverables: Extension of the kinetic theory to account for higher-order correlations, e.g. as needed in the homogeneous HMF model. Extension of the kinetic theory to account for mean-motion resonances in quasi-Keplerian systems (in galactic nuclei and proto-planetary systems), i.e. going beyond the uncorrelated double Keplerian orbit-average. Extension of the kinetic theory to account for non-resonant effects, e.g. as in the diffusion à la Chandrasekhar through local Keplerian deflections. Exploration of non-integrable geometries (e.g. thickened discs, flattened spheres, and barred discs) to account for the richness of orbits and possible chaotic diffusion. Development of a numerical solver and integrator for the linear response theory of self-gravitating systems and the associated Balescu-Lenard kinetic equation. Validation of the kinetic theory through detailed comparisons with other approaches, in particular using Vlasov solver, direct N-body methods, and FEM methods.





